Count Primes | Sieve of Eratosthenes

Count the number of prime numbers less than a non-negative number, n.

 

Example 1:

Input: n = 10
Output: 4
Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
Input: n = 0
Output: 0

Example 2:

Example 3:

Input: n = 1
Output: 0

 

Constraints:

• 0 <= n <= 5 * 106

 

Approach:

1. Create a 1D boolean array prime [] of size N.
2. Initially we presume that all numbers are prime numbers. So we will the array with true.
3. Starting from 2, we check if prime [i] is true, if so, we update every multiple of i to false.
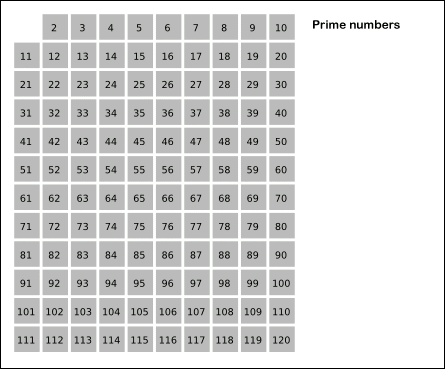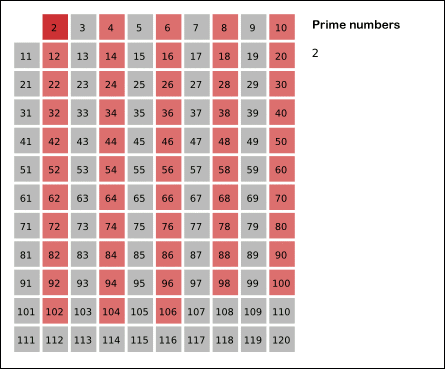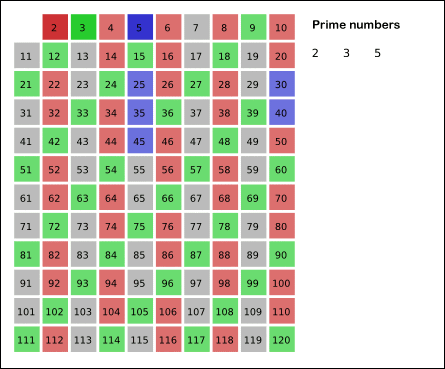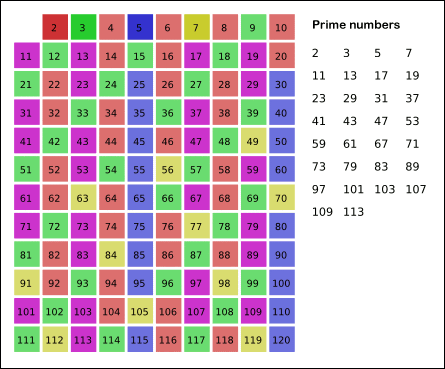
4. In the end, we check prime [] from index = 2 and print the count of cells containing the value true.
5. Note: 1 is not a prime number which is why we start iterating from 2.

TIME COMPLEXITY ANALYSIS:

Overall Time Complexity = O (N * log (log (N))

Below animation shows how the sieve will work for N = 121.

C++ Code:

class Solution {
public:
    int countPrimes(int n) {
        if (n == 0)
            return 0;
        bool prime [n];
        memset (prime, true, sizeof (prime));
        for (int i = 2; i*i < n; i++) {
            if (prime [i] == true) { 
                // Update all multiples of i to false if i is prime
                for (int j = i * i; j < n; j += i)
                    prime [j] = false;
            }
        }
        int count = 0;
        for (int i = 2; i < n; i++) {
            if (prime [i])
                count++;
        }
        return count;
    }
};

💻🐱‍💻If there are any suggestions / questions / mistakes in my post, please do comment below 👇