Flatten Binary Tree to Linked List

 

Given the root of a binary tree, flatten the tree into a "linked list":

• The "linked list" should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.

• The "linked list" should be in the same order as a pre-order traversal of the binary tree.

Example 1:

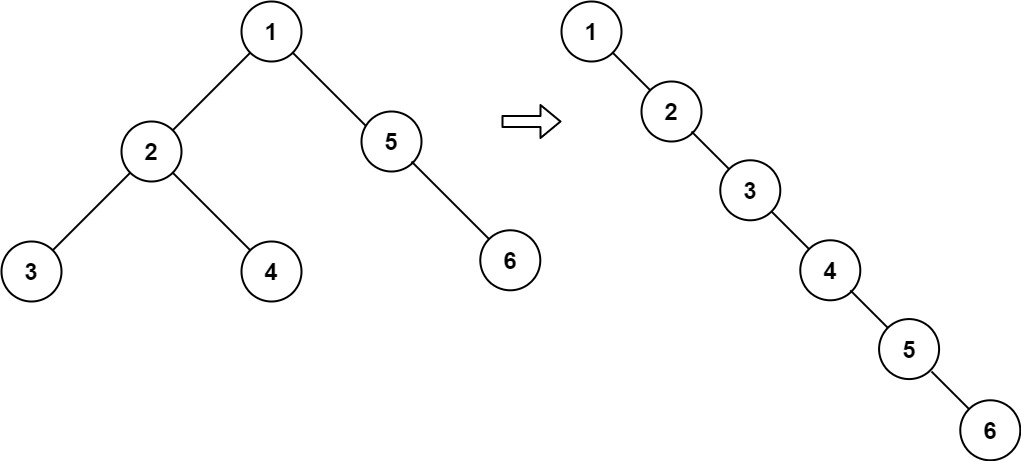
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [0]
Output: [0]

 

Constraints:

• The number of nodes in the tree is in the range [0, 2000].
• -100 <= Node.val <= 100

 

Follow up: Can you flatten the tree in-place (with O(1) extra space)?

Approach I (O(1) Space Approach):

In order to properly connect the linked list, we'll need to start at the bottom and work up. This means that we'll need to move in reverse pre-order traversal order through the binary tree. Since pre-order traversal is normally "node, left, right", we'll have to move in the reverse order of "right, left, node".

In order to complete this solution in O(1) space, we won't be able to conveniently backtrack via a stack, so the key to this solution will be to retreat all the way back up to the root each time we reach a leaf. This will push the time complexity to O(N^2).

We'll want to first set up head and curr to keep track of the head of the linked list we're building and the current node we're visiting. We'll know we're finished once head = root.

To follow the reverse pre-order traversal order, we'll first attempt to go right and then left. Since we're backtracking to root, however, we'll eventually run back into the same node that we've set as head doing this. To prevent this, we'll stop before moving to the head node and sever the connection.

Now that we can't run into already-completed territory, we can be confident that any leaf we move to must be the next value for head, so we should connect it to the old head, update head, and reset back to the root.

As noted before, once head = root, we've finished our traversal and can exit the function.

C++ Code:

class Solution {

public:

    void flatten(TreeNode* root) {

        TreeNode *head = nullptr;

        TreeNode *curr = root;

        while (head != root) {

            if (curr->right == head) curr->right = nullptr;

            if (curr->left == head) curr->left = nullptr;

            if (curr->right) curr = curr->right;

            else if (curr->left) curr = curr->left;

            else {

                curr->right = head;

                head = curr;

                curr = root;

            }

        }

    }

};

• Time Complexity: O(N^2) where N is the number of nodes in the binary tree, due to repeated backtracking to root
• Space Complexity: O(1)

Approach II (Recursive Approach):

In order to properly connect the linked list, we'll need to start at the bottom and work up. This means that we'll need to move in reverse pre-order traversal order through the binary tree. Since pre-order traversal is normally "node, left, right", we'll have to move in the reverse order of "right, left, node".

Binary tree traversal is prime ground for a recursive solution, so let's define a helper (revPreOrder) for the purpose. We'll also keep a global variable head to keep track of the head of the linked list as we work our way backwards.

Per our reverse pre-order traversal approach, we want to recursively work down the right path first then the left path, if they exist. Once we've flattened the left and right paths recursively, head should at this point be equal to the next node after the current one, so we should set it as node.right. We shouldn't forget to set node.left to null, as well.

Once we're done with the current node, we can update head to node and allow the recursion to complete and move back up to the next layer. Once the recursion stack is exhausted, head will be equal to root again.

Lastly, we have to deal with an edge case of an empty root, so we can just make sure to only call the initial recursion on root if root actually is a node. There is no need for a return statement, because the test suite will evaluate root directly.

C++ Code:

class Solution {

public:

    void flatten(TreeNode* root) {

        if (root) revPreOrder(root);

    }

private:

    TreeNode* head = nullptr;

    void revPreOrder(TreeNode* node) {

        if (node->right) revPreOrder(node->right);

        if (node->left) revPreOrder(node->left);

        node->left = nullptr;

        node->right = head;

        head = node;

    }

};

• Time Complexity: O(N) where N is the number of nodes in the binary tree
• Space Complexity: O(N) for the recursion stack, which is as long as the maximum depth of the binary tree, which can go up to N

**If you are on InterviewBit where return type is TreeNode* add return statement at last in flatten function.

return root;

💻🐱‍💻If there are any suggestions / questions / mistakes in my post, please do comment below 👇