Range Sum Query 2D - Immutable

 

Given a 2D matrix matrix, handle multiple queries of the following type:

1. Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

• NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
• int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Example 1:

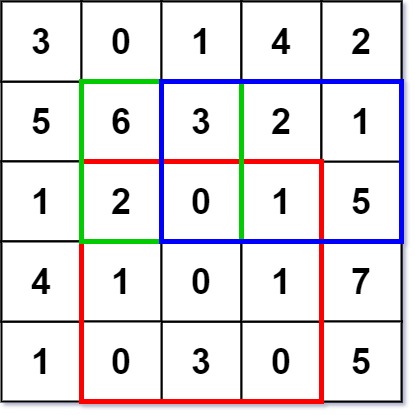
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]
Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

 

Constraints:

• m == matrix.length

• n == matrix[i].length

• 1 <= m, n <= 200

• -105 <= matrix[i][j] <= 105

• 0 <= row1 <= row2 < m

• 0 <= col1 <= col2 < n

• At most 104 calls will be made to sumRegion.

Approach I (1D Prefix Sum):

We will precompute a prefix sum for each row of the matrix in the constructor of the class. Once that's done, answering any query is as simple as iterating over all rows and computing range sum query for that row. We just sum it all and return.

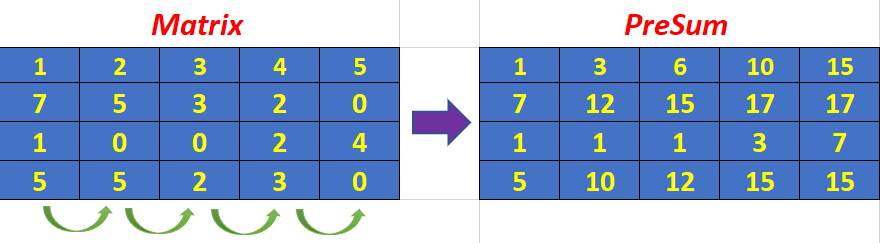
C++ Code:

class NumMatrix {
    vector<vector<int> > presum;
public:    
    NumMatrix(vector<vector<int>>& matrix) : presum(matrix) {
        // computing prefix sum for each row of the matrix and 
//storing in presum
        for(auto& row : presum) 
            for(int i = 1; i < size(row); i++) 
                row[i] += row[i - 1];                
    }    
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        // iterating over all the rows that come under query 

// region and compute range sum for each row
        for(int row = row1; row <= row2; row++) 
            sum += presum[row][col2] - 

                    (col1 ? presum[row][col1 - 1] : 0);
        return sum;
    }
};

Time Complexity :

1. Precomputation : O(M*N) , where M is the number of rows and N is the number of columns in the given matrix.
2. Query : O(R) for query, where R is the number of rows in the query region.

Space Complexity : O(M*N), to maintain the presum matrix

Approach II (Submatrix Sum Computation):

We can extend the concept of prefix sum of 1D array to the 2d matrix as well. Instead of just computing prefix sum for each row, we can compute prefix sum of a submatrix starting from (0, 0) till (row, col) for 0 <= row <= M and 0 <= col <= N.

For each cell, we will add -

• matrix[row][col] : The cell in original matrix at (row, col).

• sums[row - 1][col] : The sum of region starting at (0, 0) and ending at cell (row - 1, col).

• sums[row][col - 1] : The sum of region starting at (0, 0) and ending at cell (row, col - 1).

• -sums[row-1][col-1] : The sum of region ending at (row-1, col-1) is added twice due to above to terms. So we subtract it once. Thus, sums[row][col] will store the sum of region ending at (row, col) and starting at origin.

Similarly, while returning a query, we will use the sum of region till (row2, col2) and subtract the upper region (row1-1, col2) and left region (row2, col1 - 1) . This leads to subtraction of top-left region twice. So we add that region once (row1-1, col1-1) .

In the below implementation, I have used an extra row and column padding at the start of matrix. This simplifies the solution by avoiding any extra bounds check while computing a query. Thus, sums[i][j] will store the sum of sub-matrix ending at the cell - (i - 1, j - 1) (starting from the origin (0, 0)).

C++ Code:

class NumMatrix {

    vector<vector<int> > sums;

public:

    NumMatrix(vector<vector<int>>& m) {

        sums.resize(1 + size(m), vector<int>(1 + size(m[0])));        

        for(int r = 1; r <= size(m); r++) 

            for(int c = 1; c <= size(m[0]); c++) 

                sums[r][c] += sums[r - 1][c] + sums[r][c - 1] - 

                            sums[r - 1][c - 1] + m[r - 1][c - 1];

    }

    

    int sumRegion(int r1, int c1, int r2, int c2) {

        return sums[r2 + 1][c2 + 1] - sums[r1][c2 + 1] - 

                    sums[r2 + 1][c1] + sums[r1][c1];

    }

};

Time Complexity :

1. Precomputation : O(M*N), where M is the number of rows and N is the number of columns in the given matrix.
2. Query : O(1), since we are directly calculating sum from precomputed stored result.

Space Complexity : O(M*N), to maintain the sums matrix.

💻🐱‍💻If there are any suggestions / questions / mistakes in my post, please do comment below 👇