N Queens

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example 1:

Input: n = 4

Output: 2

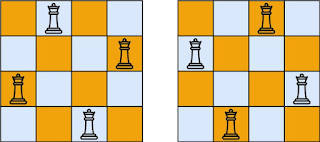
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.

Example 2:

Input: n = 1

Output: 1

Constraints: 1 <= n <= 9

Approach:

This is a common backtracking problem. We can see than the number of ways to place a N queens on a NxN board can get very large since we have N^2 choices at first, then N^2 -1, N^2 -2 and so on... leading to overall time complexity of O(N^2N).

But, we don't need to explore all O(N^2) options each time. Firstly, we have N Queens and all must be placed such that no queen attacks the other queen. This means, on each row only one queen can be placed and then we can move to the next row.

So for each row we will to place one queen without violating the constraint and then move on to the next row. This will be repeated till all N queens have been placed. We will use the check method to ensure that the queen is safe to placed at (i, j). If all N queens have been placed, we have got our first solution.

To get all the other possible solutions, we will need to remove the previously placed queen and try if its possible to place the queen on the same row at some other column, i.e, we need to backtrack. This will give us all the possible ways to place N queens on the board as per the given constraints.

A visualization from wikipedia of how this process works -

Another good visualization of N-Queens problem can be found here.

C++ Code:

int totalNQueens(int n) {
	vector<vector<bool>> board(n, vector<bool>(n, false));
	return solve(board, 0);
}
bool check(vector<vector<bool>>& board, int row, int col) {
	int n = size(board);
	for(int i = 0; i <= row; i++) {
		if(board[i][col]) return false; // checking if any queen already placed on same column previously
		// checking if all diagonals are safe -
		if(row - i >= 0 && col - i >= 0 && board[row - i][col - i]) return false;
		if(row - i >= 0 && col + i <  n && board[row - i][col + i]) return false;
	}
	return true;
}    
int solve(vector<vector<bool>>& board, int row) {
	if(row == size(board)) return 1;
	int count = 0;
	for(int col = 0; col < size(board); col++)           
		if(check(board, row, col)){          // check if we can place at (row, col)
			board[row][col] = true;          // place the queen at (row, col)
			count += solve(board, row + 1);  // explore for the next row. The function will return 1 if all N queens get placed for current combination
			board[row][col] = false;         // backtrack - remove previously placed queen and try for different columns
		}                                
	return count;
}

💻🐱‍💻If there are any suggestions / questions / mistakes in my post, please do comment below 👇