Max Area of Island

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water. 

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

Example 1:

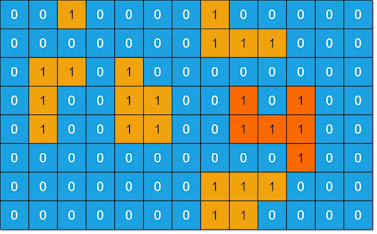
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0] ,[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]

Output: 6

Explanation: The answer is not 11, because the island must be connected 4-directionally.

Example 2:

Input: grid = [[0,0,0,0,0,0,0,0]]

Output: 0

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] is either 0 or 1.

Approach (DFS): 

So we can just use a simple iteration through the grid and look for islands. When we find an island, we can use a recursive helper function (trav) to sum up all the connected pieces of land and return the total land mass of the island.

As we traverse over the island, we can replace the 1s with 0s to prevent "finding" the same land twice. We can also keep track of the largest island found so far (ans), and after the grid has been fully traversed, we can return ans.

C++ Code:

class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int ans = 0;
        n = grid.size(), m = grid[0].size();
        for (int i = 0; i < n; i++) 
            for (int j = 0; j < m; j++)
                if (grid[i][j]) ans = max(ans, trav(i, j, grid));
        return ans;
    }
private:
    int n, m;
    int trav(int i, int j, vector<vector<int>>& grid) {
        if (i < 0 || j < 0 || i >= n || j >= m || !grid[i][j]) return 0;
        grid[i][j] = 0;
        return 1 + trav(i-1, j, grid) + trav(i, j-1, grid) + trav(i+1, j, grid) + trav(i, j+1, grid);
    }
};

Java Code:

class Solution {
    private int n, m;
    public int maxAreaOfIsland(int[][] grid) {
        int ans = 0;
        n = grid.length;
        m = grid[0].length;
        for (int i = 0; i < n; i++) 
            for (int j = 0; j < m; j++)
                if (grid[i][j] > 0) ans = Math.max(ans, trav(i, j, grid));
        return ans;
    }
    private int trav(int i, int j, int[][] grid) {
        if (i < 0 || j < 0 || i >= n || j >= m || grid[i][j] < 1) return 0;
        grid[i][j] = 0;
        return 1 + trav(i-1, j, grid) + trav(i, j-1, grid) + trav(i+1, j, grid) + trav(i, j+1, grid);
    }
}

Python Code:

class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        ans, n, m = 0, len(grid), len(grid[0])
        def trav(i: int, j: int) -> int:
            if i < 0 or j < 0 or i >= n or j >= m or grid[i][j] == 0: return 0
            grid[i][j] = 0
            return 1 + trav(i-1, j) + trav(i, j-1) + trav(i+1, j) + trav(i, j+1)
        for i, j in product(range(n), range(m)):
            if grid[i][j]: ans = max(ans, trav(i, j))
        return ans

Javascript Code:

var maxAreaOfIsland = function(grid) {
    let ans = 0, n = grid.length, m = grid[0].length
    const trav = (i, j) => {
        if (i < 0 || j < 0 || i >= n || j >= m || !grid[i][j]) return 0
        grid[i][j] = 0
        return 1 + trav(i-1, j) + trav(i, j-1) + trav(i+1, j) + trav(i, j+1)
    }
    for (let i = 0; i < n; i++) 
        for (let j = 0; j < m; j++)
            if (grid[i][j]) ans = Math.max(ans, trav(i, j))
    return ans
};

• Time Complexity: O(N * M) where N and M are the lengths of the sides of the grid

• Space Complexity: O(L) where L is the size of the largest island, representing the maximum recursion stack

• or O(N * M + L) if we create an N * M matrix in order to not modify the input

💻🐱‍💻If there are any suggestions / questions / mistakes in my post, please do comment below 👇

Leetcode: 695. Max Area of Island